CIEMAT/NIST method
The CIEMAT/NIST method is a relative or tracing activity measurement method suitable for activity determinations of pure beta, beta-gamma, pure EC and EC-gamma decaying radionuclide using a commercial liquid scintillation (LS) spectrometer.
Description of the method
by Agustín Grau Malonda, Instituto de Estudios de la Energía, 2001
The CIEMAT/NIST method is a relative or tracing activity measurement method suitable for activity determination of pure beta, beta-gamma, pure EC and EC-gamma decaying radionuclide using a commercial liquid scintillation (LS) spectrometer.
The commercial LS spectrometers have two photomultipliers working in coincidence to remove the thermal noise generated at the photocathode output of each one of the photomultipliers.
The CIEMAT/NIST method requires one to know the experimental counting efficiency of one tracer radionuclide (tritium seems to be the most adequate) for different degrees of chemical quench and to compute the counting efficiency at the photocathode output for different values of the free parameter. To obtain an universal curve, which allows one to determine the counting efficiency for any radionuclide, a model for the counting efficiency as a function of the free parameter must be developed for each radionuclide.
CIEMAT/NIST method diagram
The following diagram describes the procedure to obtain the counting efficiency for the pure beta ray emitter 14C. We consider 14C in this example but any other radionuclide can be used for the counting efficiency determination. The first step is to obtain the experimental calibration curve giving the counting efficiency ε vs. chemical quench parameter q (curve (a)), and to compute the counting efficiency ε vs. the free parameter λ for tritium (curve (b)). Since both curves have in common the counting efficiency, we can obtain the relation between the free parameter and the chemical quench parameter (curve (c)). This curve is universal in the sense that it is independent of the radionuclide but depends on the liquid scintillation spectrometer, the vial and the liquid scintillator used. The next step is to compute the counting efficiency vs. the free parameter for the radionuclide to be standardized, in our case 14C. By applying the universal curve (c) to the 14C curve (d), and taking the free parameter as a common quantity, we obtain curve (e), the calibration curve giving the counting efficiency vs. quench parameter for 14C.
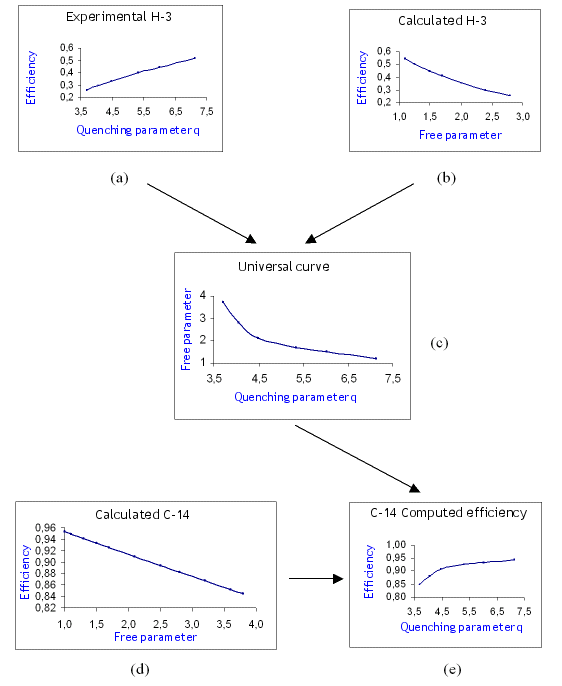
Diagram describing the application of the CIEMAT/NIST method to the standardization of 14C
(a) Experimental efficiency vs. quench curve for tritium
(b) Computed efficiency vs. free parameter for tritium
(c) Universal curve
(d) Computed efficiency vs. free parameter for 14C
(e) Computed efficiency vs. quench for 14C
Example: 14C
We measured 5 vials containing 15 mL of toluene-based liquid scintillator and a 14C radioactive solution. The measured counting rates, in counts per minute (cpm), and the quench parameters of the samples are listed in Table 1. The quench parameter, q, can be anyone of the well known external standard quantities: Horrocks H#, SQP(E) or tSIE.
Table 1. Experimental counting rate and quench factor for C-14.
| Sample | Counting rate (c.p.m) |
Chemical quench q |
| 1 | 83430 | 6,75 |
| 2 | 92012 | 5,51 |
| 3 | 30406 | 5,25 |
| 4 | 76222 | 4,20 |
| 5 | 93278 | 3,90 |
Our goal is to obtain the counting efficiency and the activity of each one of these 5 samples by applying the CIEMAT/NIST method.
We prepared and measured 6 vials containing the same volume of the same scintillator used to prepare the 14C samples and known amounts of a tritium standard solution. These sources were then gradually quenched by adding nitromethane to create a quenched set of tritium sources. The obtained calibration curve is given in table 2.
Table 2. Calibration curve of tritium
| Chemical quench q |
Counting efficiency ε |
| 7,13 | 0,5197 |
| 6,02 | 0,4474 |
| 5,34 | 0,4030 |
| 4,48 | 0,3348 |
| 4,05 | 0,2941 |
| 3,71 | 0,2560 |
Applying a computation model we have obtained the counting efficiency as a function of the free parameter for tritium. The results are shown in Table 3.
Table 3. Computed counting efficiency for selected values of the free parameter
| Free parameter λ |
Counting efficiency ε |
| 1,10 | 0,5443 |
| 1,25 | 0,5051 |
| 1,50 | 0,4474 |
| 1,70 | 0,4073 |
| 2,00 | 0,3558 |
| 2,40 | 0,3001 |
| 2,80 | 0,2560 |
Now, we take each one of the counting efficiency values for tritium from Table 2, and by interpolating into Table 3, we compute the corresponding free parameter. We apply here linear interpolation to facilitate the work. However, the best way of working is fitting a curve to the data in Table 3 or compute the counting efficiency for very close values of the figure of merit. Variations of λ of 0.005 allows one to determine the chemical quench parameter for each value of the figure of merit without interpolations. The obtained results are presented in Table 4.
Table 4. Universal curve for 15 mL of toluene based liquid scintillator
| Chemical quench q |
Free parameter λ |
| 7,13 | 1,194 |
| 6,02 | 1,500 |
| 5,34 | 1,700 |
| 4,48 | 2,122 |
| 4,05 | 2,800 |
| 3,71 | 3,710 |
The same model used to compute Table 3 can be applied to compute the counting efficiencies for different values of the free parameter for 14C. The results are shown in Table 5.
Table 5. Counting efficiencies of 14C for different free parameter values
| Free parameter λ |
Counting efficiency ε |
| 1,00 | 0,9530 |
| 1,10 | 0,9490 |
| 1,30 | 0,9409 |
| 1,50 | 0,9329 |
| 1,70 | 0,9250 |
| 2,10 | 0,9093 |
| 2,50 | 0,8938 |
| 2,80 | 0,8822 |
| 3,20 | 0,8669 |
| 3,60 | 0,8517 |
| 3,80 | 0,8442 |
We need to obtain the corresponding counting efficiency for each value of the free parameter in Table 4. This is carried out by interpolating each parameter value in Table 5. The calibration curve obtained by this procedure is given in Table 6.
Table 6. Computed calibration curve of 14C
| Chemical quench q |
Counting efficiency ε |
| 7,16 | 0,9452 |
| 6,02 | 0,9329 |
| 5,34 | 0,9250 |
| 4,48 | 0,9084 |
| 4,05 | 0,8822 |
| 3,71 | 0,8476 |
Now we can compute the counting efficiency and the activity of the samples in Table 1. By interpolating in Table 6 each chemical quench value in Table1, we obtain the corresponding counting efficiency shown in column 3 of Table 7. The activity, in KBq, can be computed from the counting rate (column 2) and the counting efficiency. The results are presented in column 4 of Table 7.
Table 7. Counting rate, counting efficiency and activity of 14C
| Sample | Counting rate (c.p.m) |
Counting efficiency ε |
Activity (kBq) |
| 1 | 83430 | 0,9408 | 1,478 |
| 2 | 92012 | 0,9270 | 1,654 |
| 3 | 30406 | 0,9203 | 0,551 |
| 4 | 76222 | 0,8815 | 1,441 |
| 5 | 93278 | 0,8669 | 1,793 |
Calculation models
The calculation models require three different sort of information: statistics, detector response and physics of the decay processes.
STATISTICS
It is assumed that the photoelectron emission at the output of the photocathode follows a Poisson law. When an electron with energy E interacts with the liquid scintillator a mean of m photoelectrons is going to be emitted by the photocathode. The probability for the emission of exactly n photoelectrons is:
\(P(n,m) = \displaystyle{\frac{m^{n}e^{-m}}{n!}}\)The photomultiplier produces a signal at the output of the anode when the number of photoelectrons emitted by the photocathode is equal or greater than 1. That means that the detection efficiency may be obtained from:
Detector efficiency \( = \displaystyle{\sum_{1}^{\infty}{\frac{m^{n}e^{-m}}{n!}}}\)
as \(\displaystyle{\sum_{0}^{\infty}{\frac{m^{n}e^{-m}}{n!}}} = P(0,m) + \displaystyle{\sum_{1}^{\infty}{\frac{m^{n}e^{-m}}{n!}}} = 1\)
Detection efficiency can also be obtained more easily from:
Detection efficiency \( = 1 – P(0,m) = 1 – e^{-m}\)
When the liquid scintillation spectrometer has two photomultipliers working in coincidence, the counting efficiency of the system, for monoenergetic particles interacting with the liquid scintillator, is the product of the detection efficiency corresponding to each photomultiplier. If we assume that the photomultipliers have identical response, the counting efficiency is:
Counting efficiency \(\varepsilon = (1 – e^{-m})^{2}\)
To compute m we define a free parameter λ as the fictitious number of electrons emitted by the photocathode in order to obtain a computed counting efficiency equal to the experimental one. The relationship between the free parameter λ, the energy E of the interacting electron and the mean number m of photoelectrons emitted by the photocathode (for a LS spectrometer of 2 photomultipliers) is given by the following equation:
\(m = \displaystyle{\frac{E\cdot Q(E)}{2\lambda}}\)where Q(E) is the ionization quench factor which will be analyzed in the next paragraph. Since the light emitted by the vial is distributed between two photomultipliers, we write 2 to take into account this light distribution.
DETECTOR RESPONSE
A characteristic of the spectrometers is their response to the interacting radiation. Liquid scintillation spectrometers present poor linearity for low energies. The ratio between energy and number of electrons at the output of the cathode is non-linear, when the energy of the interacting electrons is less than 10 keV. The non-linearity is due to the ionization quenching process.
Ionization quench depends on the concentration of the excited molecules of the solvent produced when the ionizing particle interacts with the liquid scintillator. Both excited molecules in the first singlet state or excitons S1, and those in higher singlet states Sn can contribute to the ionization quench process.
When two excitons are very close, the following reactions are highly probable:
\(S_1(1) + S_1(2) \rightarrow S_0(1) + M^{**}(2)\) \(S_1(1) + S_1(2) \rightarrow M^{**}(1) + S_0(2)\)where one of the molecules is in the fundamental state S0, while the other one is in a superexcited state M**. Superexcited states are bonded states with energy higher than the first ionization level. Consequently, the ionization quench will compete with dissociation and internal conversion to less excited electronic levels.
We have the same situation with the reactions:
\(S_n(1) + S_n(2) \rightarrow S_0(1) + M^{**}(2)\) \(S_n(1) + S_n(2) \rightarrow M^{**}(1) + S_0(2)\)The final result is the same in both situations. Excited molecules are lost and, consequently, the intensity of the flash generated by ionizing particles reduced.
In general, the response (number of fluorescence photons L(E)) to an ionizing particle which moves in a liquid scintillator is a non-linear function of the particle energy E. This non-linearity increases with the ionization power of the particle. Consequently, a beta ray of low energy will undergo higher ionization quenching than a higher energy beta ray. Birks formulated a semi-empirical model for the process and proposed the following equation for the specific fluorescence, dL/dx (number of emitted photons per unit distance along the path):
\(\displaystyle{\frac{dL}{dx}} = \displaystyle{\frac{\eta_0\frac{dE}{dx}}{1+kB\frac{dE}{dx}}}\)where η0 is the scintillation efficiency (number of fluorescence photons emitted per unit of energy), k is the rate constant for ionization quenching, dE/dx is the stopping power and B(dE/dx) is the linear ionization density.
The response is given by:
\(L = \eta_0\displaystyle{\int_0^E}\displaystyle{\frac{dE}{1+kB\frac{dE}{dx}}} = \eta_0 E Q(E)\)where
\(Q(E) = \displaystyle{\frac{1}{E}}\displaystyle{\int_0^E}\displaystyle{\frac{dE}{1+kB\frac{dE}{dx}}}\)is the ionization quench function. The computation of the ionization quench function presents three problems: the selection of the optimal value for kB, the stopping power values for energies lower than 1 keV and the composition of the commercial liquid scintillator, which atomic composition is not supplied by the firms.
PHYSICS OF THE DECAY PROCESSES
The decay process determines the equations and the nuclear constants to be used into the models. In pure beta-ray emission the statistical beta-spectrum, the relativistic Fermi factor, the correction for finite nuclear radius and the shape factor for forbidden transition are the same for all equations required in the model.
For EC, the situation is complicated by the huge number of atomic rearrangement pathways. The detection of the emitted X-rays and Auger electrons complicates the model.
The physics of the decay process is an extremely important part of the model and requires a detailed analysis of the involved processes. The books in the bibliography give an extensive description of the matter.
Bibliography
BOOKS
- L’Annunziata, M.F., Kessler, M.J., (1998) Handbook of Radioactivity Analysis. Academic Press. San Diego. California.
- Grau Malonda, A., (1999) Free Parameter Models in Liquid Scintillation Counting. CIEMAT. Madrid.
ARTICLES
- Grau Malonda, A.,(1982) Counting efficiency for electron capture radionuclides. Int J. Appl. Radiat. Isot. 33, 371.
- Grau Malonda, A., García-Toraño, E.,(1982) Evaluation of counting efficiency in liquid scintillation counting of pure beta-ray emitters. Int. J. Appl. Radiat. Isot. 33, 249.
- Grau Malonda, A. (1983) Some applications of theoretical efficiency curves in liquid scintillators. Int. J. Appl. Radiat. Isot. 34, 763.
- Garcia-Toraño, E., Grau Malonda, A. (1985) EFFY, a new program to compute the counting efficiency of beta particles in liquid scintillators.Comput. Phys. Commun. 36, 307.
- Fernandez, A., Grau Malonda, A. (1985) Uncertainties of the counting efficiency in LS solution for Fe-55. Anales de Física. B81, 161.
- Coursey, B.M., Mann, W.B., Grau Malonda, A., Garcia-Toraño, E., Los Arcos, J.M., Gibson, J.A.B. , Reher, E. (1986) Standardization of C-14 by 4pß Liquid Scintillation Efficiency Tracing with Hydrogen-3. Appl.Radiat. Isot. 37. 403.
- Garcia-Toraño, E., Grau Malonda, A. (1987) EFIGA, a Monte Carlo program to compute the interaction probability and the counting efficiency of gamma-rays in liquid scintillators. Comput. Phys. Commun. 47, 341.
- Los Arcos, J.M., Grau Malonda, A., Fernandez, A. (1987) VIASKL: a computer program to evaluate the liquid scintillation counting efficiency and its associated uncertainty for K-L-atomic shell electron-capture nuclides. Comput. Phys. Commun. 44, 209.
- Grau Malonda, A., Coursey, B.M. (1987) Standardization of Isomeric Transition Radionuclides by Liquid Scintillation Efficiency Tracing with Hydrogen-3. Application to Technetium-99m. Int. J. Radiat. Appl.Instrum. A38, 695.
- Garcia Toraño, E., Grau Malonda, A., Los Arcos, J.M. (1988) EBEGA, the counting efficiency of a beta-gamma emitter in liquid scintillators. Comput. Phys.Commun. 50, 313.
- Coursey, B.M., Lucas, L., Grau Malonda, A., García-Toraño, E.(1989) The standardization of Plutonium-241 and Nickel-63. Nucl. Instrum. Methods Phys. Res. A279, 603.
- Grau Malonda, A., (1990) Poissonian and Binomial Models in Radionuclide Metrology by Liquid Scintillation Counting. CIEMAT Report 677.Madrid.
- Calhoun, J.M, Coursey, B.M., Gray, D., Karam, L. (1991) The standardization of S-35 methionine by liquid scintillation efficiency tracing with H-3. In: Liquid Scintillation Counting and Organic Scintillators (H.Ross, J.E. Noakes and J.D. Spaulding, Eds) pp.317-323. Lewis Publishers, Chelsea, MI.
- Grau Carles,A., Martin-Casallo, M.T., Grau Malonda, A. (1991) Spectrum unfolding and double window methods applied to standardization of C-14 and H-3 mixtures. Nucl. Instrum. Methods Phys. Res. A307, 848.
- Coursey, B.M., Cessna, E., Garcia-Toraño, E., Golas, D.B. Grau Malonda, A.,Los Arcos, J.M., Martin Casallo, M.T., Schima, F.J., Unterweger, M.P. (1991) The Standardization and Decay Scheme of Rhenium-186. Int.J. Radiat. Appl. Instrum. A42, 865.
- Günther, E., Schötzig, U. (1992) Activity determination of Nb-93m. Nucl. Instrum. Methods Phys. Res. A312, 124.
- Coursey, B.M., Golas, D.B., Gray, D.H., Hoppes, D.D., Schima, F.J. (1992) Liquid scintillation standardization of Te-123m. Nucl. Instrum. Methods Phys. Res. A312, 121.
- Grau Carles,A., Rodriguez, L., Grau Malonda, A. (1993) Standardization of C-14 and S-35 mixtures. Nucl. Instrum. Methods Phys. Res. A325, 234.
- Grau Carles,A., Rodriguez, L., Grau Malonda, A. (1993) Simultaneous standardization of Sr-90-Y-90 mixtures. Appl. Radiat. Isot. 44, 1003.
- Coursey, B.M., Calhoun, J.M., Cessna, J., Golas, D.B., Schima, F.J. (1994) Liquid scintillation counting techniques for the standardization of radionuclides used in therapy. Nucl. Instrum. Methods Phys. Res. A339, 26.
- Grau Carles, A., Grau Malonda, A., Grau Carles, P. (1994) EMI, the counting efficiency for electron capture, electron capture-gamma and isomeric transitions. Comput. Phys. Commun. 79, 115.
- Grau Carles, A., Rodriguez, L., Grau Malonda, A. (1994) Standardization of I-125, Sr-85 and Cd-109 by CIEMAT/NIST METHOD. Appl. Radiat. Isot. 45, 461.
- Günther, E. (1994) Standardization of Fe-59 and I-131 by liquid scintillation counting. Nucl. Instrum. Methods Phys. Res. A339, 402.
- Galiano Casas, G., Grau Carles, A., Grau Malonda, A. (1995) CAPMULT, the counting efficiency for electron capture by a KLMN four shell model. Comput. Phys.Commun. 87,432.
- Grau Carles, A. (1995) New Methods for the Determination of Beta-Spectra Shape factor Coefficients. Appl. Radiat. Isot. 46, 125.
- Péron, M.N. (1995) Etude de la réponse lumineuse des scintillateurs liquides à des électrons monoénergétiques de basse énergie. PhD thesis, Paris-Sud University.
- Grau Carles, A., Grau Malonda. A. (1996) precision measurement of the RaE shape factor. Nucl. Phys. A596, 83.
- Grau Carles, A., Grau Malonda. A., Gomez Gil, V. (1996) Standardization of U(X 1+X2): The Th-234+Pa-234m+Th-230 mixture. Nucl. Instrum. Methods Phys. Res. A369, 431.
- Günther, E.W. (1996) A simple method for transferring the tritium calibration of an LSC system to others radionuclides. In « Liquid Scintillation Spectrometry 1994 » (G.T. Cook, D.D. Harkness, A.B. MacKenzie, B.F. Miller and E.M. Scott, Eds.) Radiocarbon 1996, 373.
- Péron, M.N., Cassette, P. (1996) Study of liquid scintillator response to low-energy electrons with a Compton coincidence experiment. Nucl.Instrum. Methods Phys. Res. A369, 344.
- Grau Malonda, A., Grau Carles, A. (1999) The ionization quench factor in liquid scintillation counting standardizations. Appl. Radiat. Isot.51, 183.
- Grau Malonda, A., Grau Carles, A., Grau Carles, P., Galiano Casas, G. (1999) EMI2, the counting efficiency for electron capture by KL1L2L3M model. Comput. Phys. Commun. 123, 114.
- Grau Malonda, A., Grau Carles, A. (2000) Standardization of electron capture radionuclides by liquid scintillation counting. Appl. Radiat.Isot. 52, 657.
- Günther, E. (2000) Standardization of Np-237 by the CIEMAT/NIST LSC tracer method. Appl. Radiat. Isot. 52, 471.
- Grau Carles, P., Grau Malonda, A. (2001) Free parameter, figure of merit and ionization quench in liquid scintillation. Appl. Radiat. Isot. 54,447.
Comments on CIEMAT/NIST method
by Ryszard Broda, Metrological Laboratory of Radioisotope Centre, Swierk, 1998.
The CIEMAT/NIST method is the widely used method for activity determination of radionuclides using tritium as a tracer. This method is very well suited for pure-beta nuclides but, in somes cases, problems connected with the ionisation quenching parameter, kB, may cause some bias in activity determination. These problems are discussed hereafter.
The quenching level of a scintillating source of a given radionuclide is generally determined using an external gamma-rays source. The Compton interaction spectrum recorded with the source is used to calculate a quenching index, QI. The definition of this index depends on the counter manufacturer. This index could be, for example, the Horrocks number (H*), the SQPE index or the TSIE index.
The counting efficiency of tritium εH for a given quenching index, is determined after the measurement of a set of quenched tritium standards. The theoretical calculation of the counting efficiency of tritium leads to the determination of the figure of merit η0, related to the observed εH. The counting efficiency of the source of a given radionuclide εNuc are then calculated. In this calculation, a model of the ionisation quenching phenomenon is taken into account. This model is generally the Birks function. This calculation procedure can be resumed schematically as follows :
On the ground of the theoretical calculation of coincidence counting efficiency as a function of η0 (an example is presented in Fig.1) it appears that the procedure (1) leads to different values of counting efficiency εNuc, for the one εH, depending on the value of the kB parameter taken into account for a given source.
For example, the calculation was performed for 55Fe with two different kB values, for one selected εH. Two different theoretical values of counting efficiency εFe were obtained, as presented in Fig.2. Other results for 14C, 54Mn and 55Fe are listed in Table 1. Relative discrepancies (D) of calculated extreme counting efficiencies (for kB = 0.006 cm/MeV and kB = 0.012 cm/MeV) are given.
Thus a systematic bias of the CIEMAT/NIST method appears if the kB value is not exactly known for a given source. One can see that, even in the case of a high counting efficiency like 14C, this bias could be around 1 or 2%. For low counting efficiency nuclides, this bias could be ten times higher.
Things are going dramatically worse in the case of 55Fe or 54Mn activity measurement where the systematic errors on the activity could reach several percents.
Günther [1] has reported an essential modification of the CIEMAT/NIST method. For 55Fe activity measurement he used 54Mn as a tracer instead of 3H. Good results of this approach are comprehensible on the basis of our calculation, as the similarities of the functions εMn(η0, kB) and εFe(η0, kB) in the measurement range is visible. Moreover Günther has performed additional measurements using a 55Fe standard source for the direct determination of the ionisation quenching parameter value, kB. If this value is not exactly known, a systematic error could reach a few tenth percent, as can be seen in Table 2.
In conclusion it seems that there could be a bias in the activity determination using the CIEMAT/NIST method if the kB parameter value is not known for a given source. This error decreases with the increase of the detection efficiency.
Bibliography
[1] E. Günther, Standardisation of the EC nuclides 55Fe and 65Zn with the CIEMAT/NIST LSC tracer method, (Conference paper No.005, ICRM’97).Tables and figures
Table 1. Differences of the results of the CIEMAT/NIST method for 14C, 55Fe and
54Mn for different values of the kB parameter
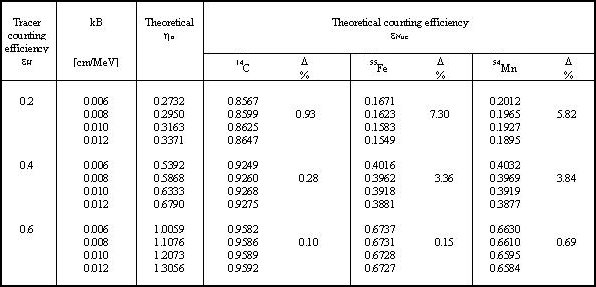
Table 2. Differences of the results of the CIEMAT/NIST method for
55Fe with 54Mn as a tracer for different values of the kB parameter
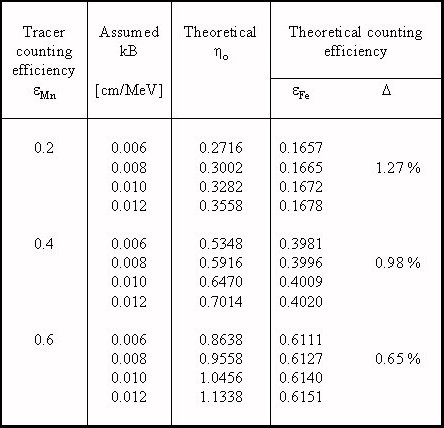
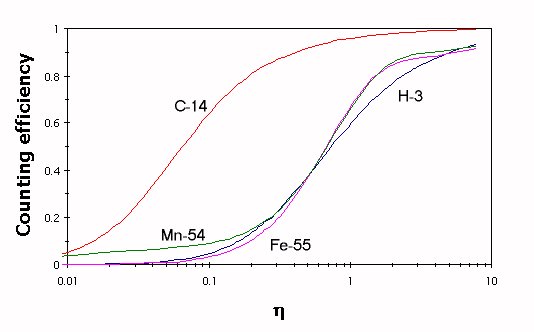
Fig.1. Counting efficiencies for 3H, 14C, 54Mn and 55Fe as a function
of η0 for Ultima Gold liquid scintillator and kB = 0.006 cm/MeV.
